Alright...here we go.
I work in a district where all math courses 7th-Geometry have retests; it is not the teacher's choice. That being said, I love retesting! My students learn so much, about math and study habits in general, between their first test and their retest.
Here is an overview of how retesting looks in my classroom.
All tests are written as a team and all courses give the same tests throughout the district. This helps to ensure that our students receive an equitable education. As we write the tests, we write them with testing/retesting in mind. Meaning, we write small sections with about one or two topics addressed per section. These are called competences or objectives. Most unit tests have 3-4 competencies of new material. Beginning on the second unit, we also include a review competency. These questions help keep ideas fresh throughout the year. So most tests are 4-5 competencies long. Every once in awhile we have a 6-comp doosey, but we try to avoid that.
During the unit students complete qualifiers. These are particular activities/investigations/homework assignments/projects that will qualify them for specific sections of the retest later on. In my classroom, we do lots of activities and assignments that are not qualifiers as well. I specifically tell students which assignments are qualifiers and which are not; I'm all about transparency! After I grade a qualifying assignment, I give it back to students and they record the grade on their grade sheet for the appropriate competency. You can see a copy of my grade sheet in this post. Like I said, we do other things that are scored, they are just not recorded on the grade sheet. I require that every qualifying assignment have a grade of at least an 80%. If a student receives less than an 80% they must correct the incorrect work and resubmit their work. I give full credit for resubmitted work. This also relieves a lot of the stress students feel and insecurity about having one shot to complete their math homework. They go home, they try, we discuss it again the next day, they submit their work, I offer feedback, they tweak and resubmit. I really like the system.
Anyway...moving on.
After an entire unit is complete, students do a review assignment and take their test. Each competency of their test receives a separate score out of 100 points. I hand back their tests and they record their competency scores. Any competencies that they scored at least an 80 on are considered "mastered" meaning they do not have to retest. They are welcome to try for a higher score, but they do not have to. Any competency where they scored lower than an 80, they are required to retest.
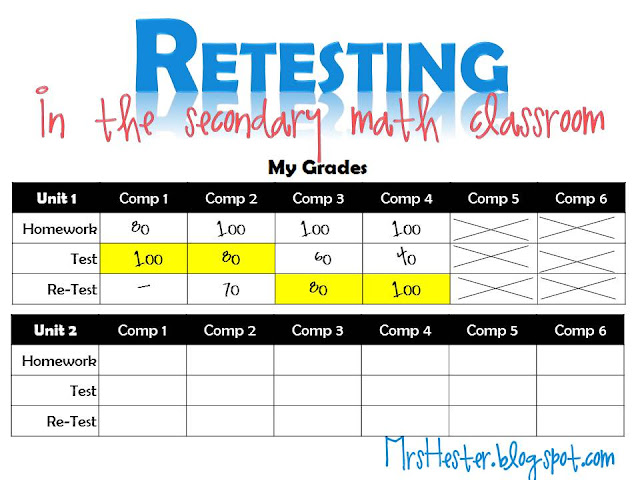
As an example, a grade sheet would be looking something like this right now.
This particular student would need to fix their qualifying assignment for competency 4, since it is lower than an 80%, in order to qualify for their retest. 
I really like that my grade sheet shows homework and test scores for the same material stacked vertically. It is a very often occurrence that when a student makes a low test score, such as a 40, they also have a relatively low homework score. They can see their hard work (or lack thereof) really paying off.
I give students about a week between tests. During this time we go over common errors and misconceptions and I hold tutoring times during seminar (a 40 minutes block built into our day for tutoring, homework, and assemblies). I also remind students repeatedly throughout this week to check their grade sheets and make sure they are qualified. I will often create a second review-type assignment before the retest that also counts as a qualifier.
Once it is retest day, students turn in any qualifying assignments. These are often homework assignments they have been correcting to get their 80%. This also includes any test corrections that I assign for a particular unit. As students take their test, I quickly check the assignments that have been turned in, update their homework grades, and make sure every student that is taking a test is qualified for their test.
After their retest, we go over final errors and students record their retest scores. The sample grade sheet would look something like this now.
Notice the student fixed their 70 in comp 4 and was allowed to retest that section. They did not retest comp 1 since they scored a 100 the first time. They tried to improve their comp 2-4 scores and succeeded in comps 3 and 4. I always keep the highest grades that students make in each section. So in this case, I would keep the highlighted 80 for comp 2 since their retest score was lower. Students usually like to calculate their overall grade, in this case 360/400, or 90%. I keep each competency score separate in my grade book.
Since this style is fairly repetitive, I also give a problem-based task for each unit that forces students to look at the material in a new way. Those tests do not have a retest opportunity and are worth half the points of the mastery test. In this case, since the mastery tests were worth 400 points the task would be worth 200 points. All of those scores are recorded at the bottom of the grade sheet in their own section.
I hope that answers some of your questions! Feel free to comment with more questions and I'll do my best to answer them.
Also...
Get your copy of my grade sheet here! I created the original file in publisher, email me if you want a copy of that one.